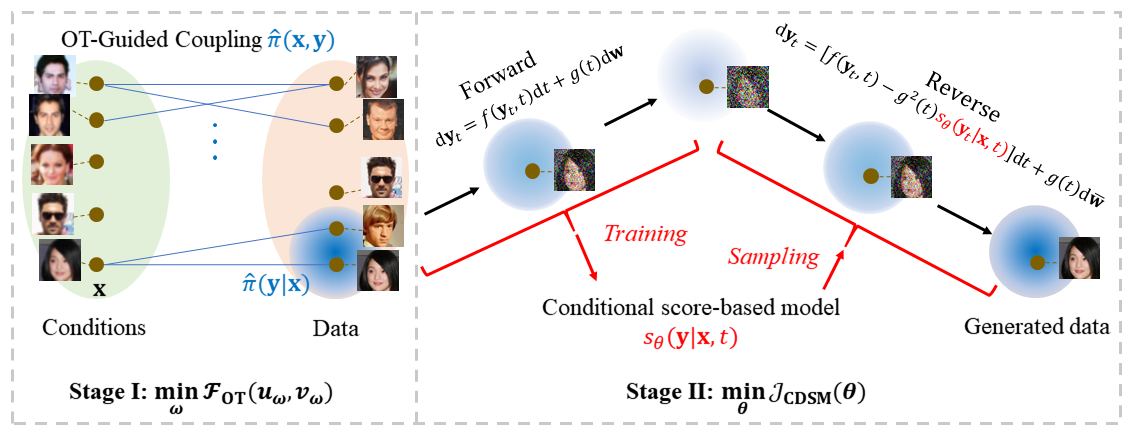
Unpaired Super-resolution Problem
In unpaired super-resolution, we are provided two sets of images of low-resolution and high-resolution, respectively. In traditional paired super-resolution, the low-resolution and high-resolution images are one-to-one paired. By contrast, in unpaired super-resolution, there lacks coupling relationship (e.g., one-to-one relationship) between low-resolution and high-resolution images (see the figures below). Unpaired super-resolution is more realistic in real-world applications, because collecting one-to-one paired images with the same content is not easy.
The goal of unpaired super-resolution is to train an AI model using the unpaired datasets such that it can output the high-resolution image for a test low-resolution image in inference.